Necessary Background

This visualization is going to take a bit of explaining. Mapping the internet is a question that has intrigued folks who are worried about internet security, the digital divide, robustness, even artists who just wonder about all those bits of information flowing around us.

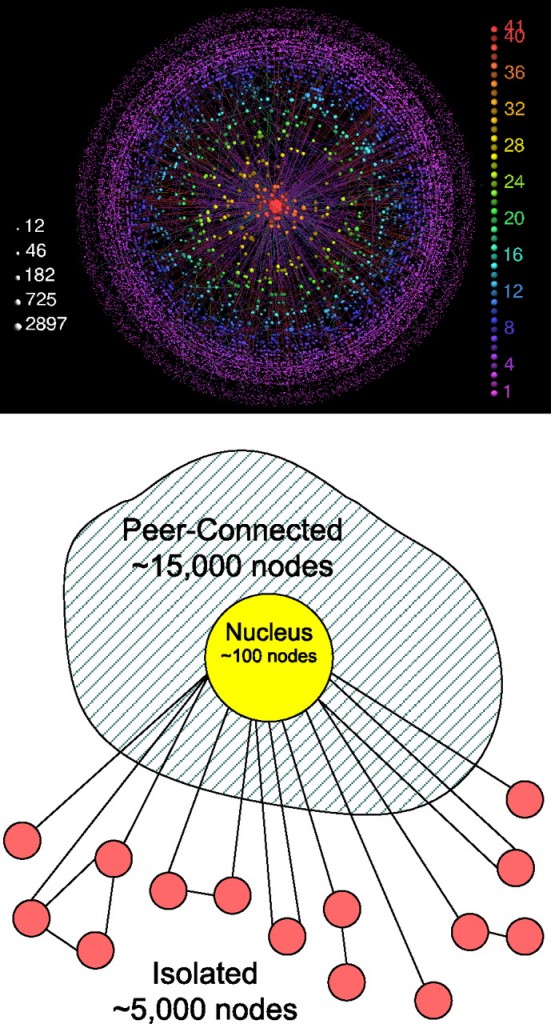
This visualization attempts to describe the structure of the internet as a network, not to map its black holes, censorship holes or describe actual geographic nodes like Akamai in yesterday’s post. This is a different sort of map and it requires some background reading. The authors set up a strategy for exploring the network terrain of the internet that generated these three areas – the central nucleus area consisting of the most highly connected nodes, a fringe around the edges of a whole bunch of pages that would be cut off completely if the nucleus were removed, and then a sort of spongy area in between these extremes full of nodes that could connect to each other if the nucleus were removed but not nearly as efficiently. Call it the peer-to-peer zone.

Here’s how the authors described the process that generated the three classes of nodes:

First, we decompose the network into its k-shells. We start by removing all nodes with one connection only (with their links), until no more such nodes remain, and assign them to the 1-shell. In the same manner, we recursively remove all nodes with degree 2 (or less), creating the 2-shell. We continue, increasing k until all nodes in the graph have been assigned to one of the shells. We name the highest shell index k max. The k-core is defined as the union of all shells with indices larger or equal to k. The k-crust is defined as the union of all shells with indices smaller or equal to k.

Even if you don’t spend your days dividing networks into k-shells, I hope you now understand that this model’s strength comes from the fact that the structure was generated rather than imposed by initial assumptions. There were no initial assumptions.

What Works

Success here is that people who do not study networks can understand what these researchers did at all. Most highly specialized research (and pretty much all research is highly specialized) only makes sense to the people occupying the sub-sub-discipline actively working on those questions, equipped with the right language, fully immersed in the discourse of the niche. That would have been true if I had just tried to read this article without the accompanying image.

I also think it helps immensely to see the sketchy, comparatively unglossy schematic along with the polished final image. The glossy version adds in enough detail that I might have missed the big picture without having the schematic there to remind me that it isn’t about color or distance – that the contribution is all about the three types and their relationship to one another.

What Needs Work

Similar problem with this image as I had with yesterday’s image: the final image is so glossy and sealed that I feel like it’s hiding something. The more gloss on an image, the more it becomes impenetrable to critique. It presents itself as hermetically sealed – how can anyone get under the skin and assure themselves that this is a trustworthy image? This glossiness of the final image is probably why the schematic has so much appeal. It’s easier to see how the two were put together and *why* it is the way it is.

Aesthetically, I am not sure I like the colors and I think I would have tried to achieve the look of a solid core, a very fringe-y outer layer that has more volume but is almost insubstantial in its lacy-ness, and then a middle layer that sort of looks like a network made of jello. It is so easy to say these things when you don’t have to kill yourself in photoshop and illustrator making them happen.

Note

[There is another post on Graphic Sociology about mapping the internet about visualizing the map of an individual site which is here.]

Relevant Resources

Carmi, Shai; Havlin, Shlomo; Kirkpatrick, Scott; Shavitt, Yuval; and Shir, Eran. (2007) “A model of Internet topology using k-shell decomposition” Proceedings of the National Academy of Sciences of the United States of America.

Moskowitz, Clara. (11 April 2008) Black Holes Charted on the Internet. msnbc.com, Technology and Science.

Reporters Without Borders (2007) Internet Black Holes.

Wachowski brothers (directors, writers) The Matrix.